Leetcode 刷题板子

2023/8/9 code

一些刷题板子

C++

小心数组下标越界，这个不报错！！！

然后memset只能输入0、1

pop()没有返回值

substr()是位置与长度！！

然后做题时记得检查边界条件以及末尾！！

#include<vector>
#include<algorithm>

//vector赋值而不是传递引用
vector<int>vec(n);
length=vec.size();
vec.push_back(12);/末尾加入12; 
vec.pop_back();// 弹出最后一个元素
vec.empty();//判断是否为空
vec.insert(1,aaa);
vec.erase(4)
指针nullptr
    
sort(a,a+n)表示对a[0]~a[n-1]排序
    
stack:
stack<int>mystack;
stack.push(1);stack.pop();stack.size();
deque:
deque<int>mydeque;
deque.size()
deque.empty();deque.back();deque.push_back(1);deque.pop_back()//最后一个元素
deque.front();deque.push_front();deque.pop_front();

auto lambda函数：

auto fun =[](int x){return x*x;};//特点就是不需要返回值
auto fun=[&](int a,int b){int temp=b;b=a;a=temp;};//这里lambda函数传递引用

function<int(int,int)> fun=[&](int x,int y)->int{
    ... 
};

二维数组排序：

static bool cmp(vector<int> a, vector<int> b)
{
    if(a[0] != b[0]) return a[0] > b[0];
    if(a[1] != b[1]) return a[1] > b[1];
    if(a[2] != b[2]) return a[2] > b[2];
}
 
int main()
{
    vector<vector<int>> vec = { {1,4,3}, {1,4,7} , {1,3,5} , {2,9,4} , {2,5,8} , {3,9,6} };
    
    sort(vec.begin(), vec.end(), cmp);
 
    for(auto p : vec)
        cout<<p[0]<<' '<<p[1]<<' '<<p[2]<<endl;
 
    return 0;

优先队列：

priority_queue<myclass,	vector<myclass>,cmp>pq;
pq.push();pq.pop();pq.top();pq.empty();

//cmp类：
class cmp{
  bool operator(myclass c1,myclass c2){
      return c1.time<c2.time//升序排列，否则降序
  }  
};

//正常队列pq：
pq.push();pq.pop();pq.front();pq.back();

结构体用法：

struct robot{
    int pos;
    int idx;
    int health;
    robot(int pos,int idx,int health):pos(pos),idx(idx),health(health){}
};

然后对下表进行排序可以这样：

iota(arr,arr+n,0);
sort(arr,arr+n,[&](int i,int j){
   return pos[i]<pos[j]; 
});

需要注意的是面对多维数据关联的情况，我们可以考虑只关注下标（比如说把下标压入栈中，而不是把值压进去）

字符串

isdigit()  isalpha()
s.substr(pos,len)//跟java不一样！！！
new_str=String(str.rbegin(),str.begin())

算法思想分析

CSP 202212-3 关于棋盘对角线Z字形遍历问题处理：

for(int i=0;i<2n-1;i++)
    for(int j=0;j<=i;j++){
        int x=i%2==0?i-j:j;
        int y=i%2==1?i-j:j;
        if(x>=n||y>=n) continue;
        arr[x][y]=input[idx];idx++;
    }
//思考就是直接对对角线遍历，然后选择棋盘内点进行赋值

最小割最大流：

想法：从最大的边开始，一条一条往图里面加边。一旦两个点在加了边A之后变成连通，那么该边A的值就是这两个点的最小割最大流。维护图的连通性可以使用并查集。

线段树与树状数组：

树状数组：给定区间[a,b] 用于处理多次修改值时求其中子区间和的问题。我们用中间数组V[n]记录局部和。

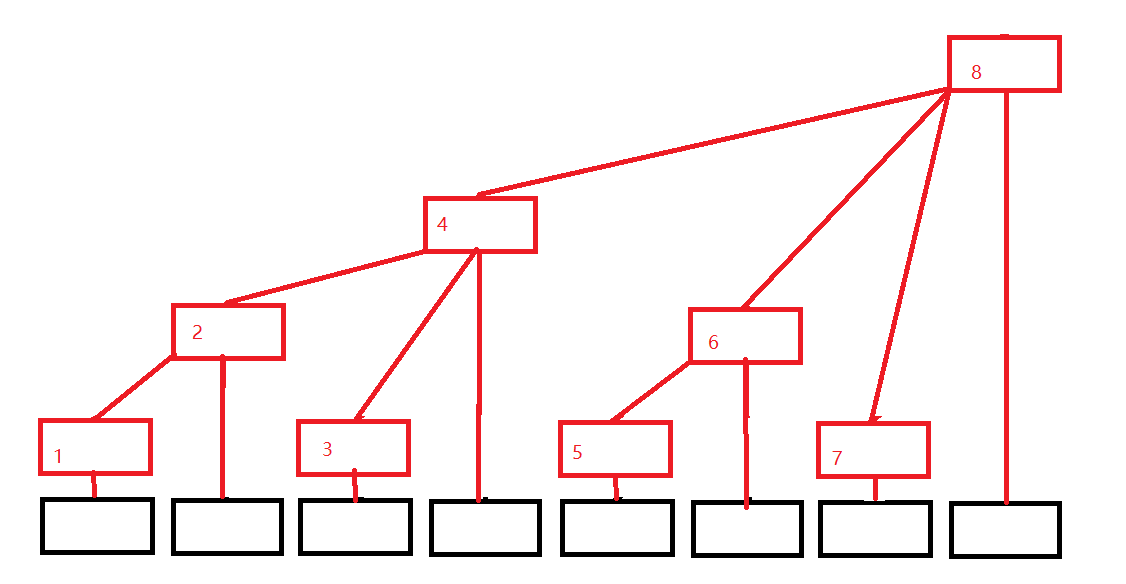
int lowbit(x){return x^-x}  //用于求出x内只保留末尾1的数
//首先：对xi更新意味着我们需要对一系列Vn进行更新，然后为了求出子区间和，我们利用前缀和化成求Si的问题。
//在位置i加k：
void update(int i,int k){
    while(i<=n){
        v[i]+=k;
        i+=lowbit(i);
    }
}
int getsum(int i){
    int sum=0;
    while(i>0){
        sum+=v[i];
        i-=lowbit(i);
    }
    return sum;
}

计算几何：

线段相交：AB:(x1,y1) (x2,y2) CD:(x3,y3) (x4,y4)

充要条件：

$1.\quad (AC \times AB)(AD \times AB)<0 \quad(1)\quad (CA \times CD)(CB \times CD)<0 \quad(2)$

$2. \quad (1)或(2)式子有一个取等,或者全取等而且min(x3,x4)>max(x1,x2)（此时意味着两线段共线）$

$注意到AC \times AB=0表示平行,<0表示AB在AC顺时针方向180^{\circ}内,>0则相反$

二分查找模板：(<就h掉，>就l增)

//<=a 的max:
int l,h,mid=(l+h+1)/2;
while(l<h){
    if(arr[mid]>a){
        h=mid-1;mid=(l+h+1)/2;
    }
    else{
        l=mid;mid=(l+h+1)/2;
    }
}

//>=a的min

int l,h,mid=(l+h)/2;
while(l<h){
    if(arr[mid]>=a){
        h=mid;mid=(l+h)/2;
    }
    else{
        l=mid+1;mid=(l+h)/2;
    }
}

LOADING

Leetcode 刷题板子

C++

算法思想分析